Drawing a Binary Tree in CoffeeScript
A few months ago I wrote a small CoffeeScript program to draw binary search trees on a web page page using the HTML 5 Canvas element and was very pleased with clarity and structure of the resulting code. This blog post elaborates on the code structure and how it compares to previous implementations of the same idea that I have done in other languages.
I’ve written programs to draw binary search trees before in C# and Ruby and I wasn’t sure how a CoffeeScript implementation would compare against implementations in more traditional object oriented programming languages. Thanks to CoffeeScript’s support for classes the structure of this implementation is pretty much as you would expect: a BinaryNode class to hold node data, a BinaryTree class to implement the basic binary search tree operations (add, walk), and a BinaryTreeDrawer to calculate the coordinates where each of the nodes should be drawn.
In addition, since this project requires only client-side code (I don’t store the binary search tree data in a server database) it’s was very pleasant not having to deal with a context switching between a “client side” mental model and a “server side” one. This is uncommon in real life projects but it was a nice bonus for a pet project like this.
You can see a running version of this project here. The full CoffeeScript (and JavaScript) source code is available on github.
Binary Tree or Binary Search Tree
Properly speaking the code in this blog post implements a Binary Search Tree (BST) which is a more specific version of a Binary Tree. Cormen et al. give a good explanation of this on their book Introduction to Algorithms. Binary trees are trees in which each node has at most two children, one of them called "left subtree" and the other called "right subtree" but there is no order enforced per-se (pp. 1178). Binary Search Trees on the other hand are always stored in a way as to satisfy the binary-search-tree property (pp. 287):
Let x be a node in a binary search tree.
If y is a node in the left subtree of x, then y.key ? x.key.
If y is a node in the right subtree of x, then y.key ? x.key.
I took a bit of a liberty on this blog post (and its related source code) and use both terms interchangeably. Please be aware that all of the references to binary tree in this blog post are in fact references to binary search trees.
Basic Structure of the Code
The main classes that I used to implement the binary search tree drawer functionality are BinaryNode, a BinaryTree, and a BinaryTreeDrawer.
The BinaryNode class is just a small “data class” that stores the information about each node, namely the value of the node and pointers to the node to the left and right of it (gist).
class BinaryNode
constructor: (@value) ->
@left = null
@right = null
root = exports ? window
root.BinaryNode = BinaryNode
The BinaryTree class implements the functionality to add nodes to the tree and walk the tree. The add method takes care of adding each new value to the tree and updating the other nodes accordingly. The walk method goes through each node of the tree in-order and calls another function to allow you to decide what to do on each node (e.g. print it to the screen.)
The code for this class is shown below. Notice that this is just a partial implementation of a binary search tree since it only implements the add and walk methods but is missing functionality to remove nodes, search for values, find the min and max values in the tree, et cetera.
{BinaryNode} = require?("./binary_node") or window
class BinaryTree
constructor: (rootValue) ->
@root = new BinaryNode rootValue
@count = 1
add: (value) ->
newNode = new BinaryNode value
node = @root
loop
if value >= node.value
if node.right is null
node.right = newNode
break
else
node = node.right
else
if node.left is null
node.left = newNode
break
else
node = node.left
@count++
walk: (callback) ->
@walkFromNode(callback, @root)
walkFromNode: (callback, node) ->
@walkFromNode(callback, node.left) unless node.left is null
callback(node)
@walkFromNode(callback, node.right) unless node.right is null
toString: ->
values = []
@walk (node) -> values.push node.value
values.join(', ')
root = exports ? window
root.BinaryTree = BinaryTree
The BinaryTreeDrawer class walks through the nodes of the tree and calculates the coordinates where each of them should be drawn. This class does not draws the tree per-se, rather it calls a function of your choosing with the coordinates where the node should be drawn.
{BinaryTree} = require?("./binary_tree") or window
class BinaryTreeDrawer
constructor: (@tree, @distanceX=20, @distanceY=20) ->
# Draws a binary tree (always starts at the root)
draw: (x, y, callback) ->
@drawNode @tree.root, x, y, callback
# Draws a binary tree starting at the specified node
drawNode: (node, x, y, callback) ->
return if node is null
callback node.value, x, y, x, y
@drawLeft node.left, x, y, callback unless node.left is null
@drawRight node.right, x, y, callback unless node.right is null
drawLeft: (node, parentX, parentY, callback) ->
if node.right is null
count = 0
else
count = 1 + @childrenCount node.right
x = parentX - @distanceX - (count * @distanceX)
y = parentY + @distanceY
callback(node.value, x, y, parentX, parentY)
@drawLeft node.left, x, y, callback unless node.left is null
@drawRight node.right, x, y, callback unless node.right is null
drawRight: (node, parentX, parentY, callback) ->
if node.left is null
count = 0
else
count = 1 + @childrenCount node.left
x = parentX + @distanceX + (count * @distanceX)
y = parentY + @distanceY
callback node.value, x, y, parentX, parentY
@drawLeft node.left, x, y, callback unless node.left is null
@drawRight node.right, x, y, callback unless node.right is null
childrenCount: (node) ->
count = 0
count += 1 + @childrenCount node.left unless node.left is null
count += 1 + @childrenCount node.right unless node.right is null
count
root = exports ? window
root.BinaryTreeDrawer = BinaryTreeDrawer
Console Application
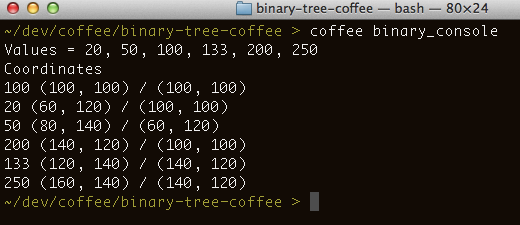
File binary_console.coffee shows a very sample of usage of the BinaryTree and BinaryTreeDrawer classes. This console application creates a binary search tree, adds a few nodes to it, and outputs to the console the coordinates where each of these nodes should be drawn.
# Node.js console demo program for the BinaryTree and BinaryTreeDrawer
{BinaryTree} = require('./binary_tree')
{BinaryTreeDrawer} = require('./binary_tree_drawer')
# Create a binary tree
tree = new BinaryTree(100)
tree.add 20
tree.add 50
tree.add 200
tree.add 133
tree.add 250
console.log "Values = #{tree.toString()}"
# "Draw" the tree (i.e. output each nodes' coordinates to the console)
console.log "Coordinates"
drawer = new BinaryTreeDrawer(tree)
drawer.draw 100, 100, (v, x1, y1, x2, y2) ->
console.log "#{v} (#{x1}, #{y1}) / (#{x2}, #{y2})"
If you have CoffeeScript installed on your box you can just run “coffee binary_console” and you’ll see an output similar to this:
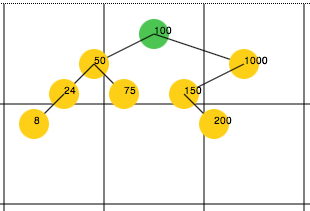
The Demo Web Page
Once I implemented the BinaryTreeDrawer it was easy to hook this to a web page and actually draw a binary search tree using the HTML 5 Canvas element. The callback passed to the drawer code in this case actually draws circles and lines for each node rather than just outputting the result to the console. Below is a snippet of the code found in binary_web.coffee that shows the basic code to draw the tree:
drawNode = (v, x1, y1, x2, y2) -> rootNodeColor = "#4CC552" # green lastNodeColor = "#ADDFFF" # blue nodeColor = "#FDD017" # yellow color = nodeColor color = rootNodeColor if x1 is x2 and y1 is y2 color = lastNodeColor if v is lastValueAdded drawLine x1, y1, x2, y2 drawCircle x1, y1, nodeSize, color drawLabel x1, y1, v $ -> # initialize the binary tree with some data.. tree = new BinaryTree 100 tree.add 1000 tree.add 50 tree.add 150 tree.add 75 tree.add 200 tree.add 24 tree.add 8 offsetX = 30 offsetY = 30 drawer = new BinaryTreeDrawer tree, offsetX, offsetY startX = canvasWidth / 2 startY = 30 drawer.draw startX, startY, drawNode
Final Thoughts
As I said at the beginning of this blog post, I was very pleased with how succinct the code in CoffeeScript to implement a binary search tree drawer ended. The clear and concise CoffeeScript syntax aided with CoffeeScript support for a traditional way of defining classes (while behind the scenes using JavaScript prototypes) resulted in code that is both easy to write, test, and maintain.
Related posts
- A review of Learning JavaScript Data Structures and Algorithms (2015)
- Drawing a Binary Tree in Ruby (2011)
- Binary Tree in C# (2006)